The Integral

represents area bounded by the curve x=f(y)
on one side, the line y=c and y=d on other two sides, y-axis on the fourth
side.
If
the area lies left of y-axis 
gives negative value as area. Therefore
the formula in such
case
is, Area=  or
or 
When
using Integrals to find the Area we always get the area between the curve and
the axis (dx or dy). For example, (refer the figure below) while finding area
bounded by a parabola open upwards from x=a to x=b and x-axis we will not get
area A1 but we arrive at area A2.
If the Area under consideration lies above as well as below
x-axis (see figure below), then you have to find area like this,

or

 represents
area bounded by the curve y=f(x) on one side, the line x=a and x=b on other two
sides, x-axis on the fourth side.
represents
area bounded by the curve y=f(x) on one side, the line x=a and x=b on other two
sides, x-axis on the fourth side. 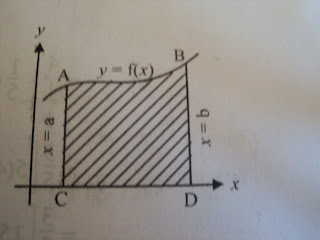






No comments:
Post a Comment