A Set is a collection of objects.
In maths it is a collection of numbers.
A Cartesian Product is combination of 2 or more sets. it is represented as AxB
for example A={a,b,c} B={1,2,3}
then AxB={(a,1) (a,2) (a,3) (b,1) (b,2) (b,3) (c,1) (c,2) (c,3)}
A Relation is a subset of AxB.
The first set is called Domain.
Second Set is called Co-domain.
In other words a Relation is a random combination of elements of Domain to Co-domain.
A Function is special relation which should follow 2 rules.
1. No element should be leftout in domain without mapping. ie., all elements in the
domain should be in relation.
2. one element in domain cannot be mapped to two or more elements in
co-domain. (note. But two or more elements in the domain can be mapped
to one element in the co-domain.)
Note: All Functions are Relations but all Relations are not Functions.
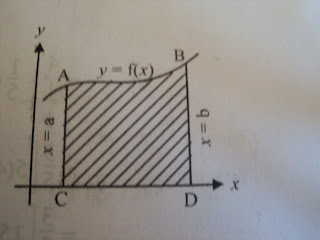
 represents
area bounded by the curve y=f(x) on one side, the line x=a and x=b on other two
sides, x-axis on the fourth side.
represents
area bounded by the curve y=f(x) on one side, the line x=a and x=b on other two
sides, x-axis on the fourth side.